ch’Árijská aritmetika
ch’Árijská aritmetika je předmět, který učí počítat s obrazy, na rozdíl od tzv. moderní matematiky, která počítá s abstraktními čísly, tj. nesrozumitelně. Čísla nenesou žádné obrazy, takže dochází ke zmatkům a děti mají potíže s pochopením toho, co se nyní učí od 1. třídy. Proč bychom měli studovat ch’Árijskou aritmetiku a nikoli da’Árijskou, Rassénskou nebo Svatoruskou? Protože ch’Árijská pokrývá všechny tři aritmetiky, plus další prostorové rozměrnosti, časové struktury a objemové. Naši Předci používali ch’Árijskou aritmetiku v každodenním životě k určení: hmotnosti, objemu, plochy, váhy, struktury, pro stavebnictví.

Podívejme se na znaky používané v ch’Árijské aritmetice, některé jsou typické pouze pro tuto naší aritmetiku.
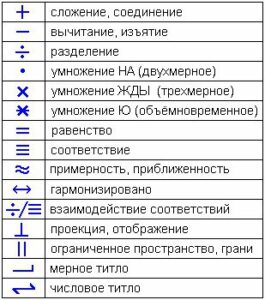
„+“ sčítání.
„-“ odčítání, odebírání. Odečíst znamená něco odebrat.
„÷“ rozdělení. Nejedná se o dělení, ale o rozdělování. Čára „odčítání“ oddělila dva body, je to, jako bychom jeden odečetli nahoru a druhý dolů, tj. rozdělili je podle příslušného pořadí.
«•» násobení Na (dvourozměrné).
N – Náš, A – Az – člověk s myslí v 16. rozměrnosti.
To znamená, že násobení Na je násobením Našich Předků, kteří žili na Zemi, tj. prováděli své výpočty na nějaké rovinné formě. Protože je to na rovině, znamená to, že je to dvourozměrná násobilka.
«х» násobení Ždy (trojrozměrné). Přes jeden bod byly vedeny čtyři přímky, čtyři prostorové souřadnice. V Judžismu máme: Tři sloni a želva – svět jakoby trojčlenný, ale tato trojčlenná struktura spočívá na čtvrté (na želvě). Proto jsou v „křížovém násobení“ čtyři linie, jsou to hloubka, délka, výška a současně v čase. Proto se náš Svět nazývá čtyřrozměrný (trojrozměrný ve čtvrtém).
Ž – „život“, D – „dobro“, Y – „podléhající určitým pravidlům“. To znamená něco dobrého stvořeného v životě, podléhajícího určitým pravidlům. Vše je určeno Kony Javi, takže vše je trojrozměrné, ale v čase, protože vše se děje, vše plyne.
«х-» násobení Ju (objemovo-časové). V zápisu zůstává „křížové – násobení „Ždy“, tj. stejné charakteristiky, ale vodorovnou čarou je rozdělujeme od sebe. To znamená, že pokud znak „rozdělení“ rozděluje řády různých struktur, zde je rozdělujeme na stejné struktury, dostáváme objem rozdělený v čase. Objemové a prostorové.
Podívejte se na Ю (Ju): je zde kruh (objem) a něco je mimo něj, takže objem je časový i prostorový. Jsouce na kouli vnímáme rovinu a jsouce na rovině vnímáme kouli.
«=» Rovnost. Jedna čára je „odčítání“ a dvě čáry jsou již odečteny a vypočteno, co dostaneme. Ale rovné objemy si nemusí být rovny, takže máme znak shody.
«≡» shoda. Příklad: Dvě litrové láhve, v jedné je třešňový džus, v druhé mléko. Lahve jsou si rovny objemem, ale nejsou si rovny hodnotou. Zavádíme další výpočetní charakteristiku. Protože nejsou stejné, ale shodné, znamená to, že odpovídají určité struktuře. Proto se k rovnosti přidává další vlastnost – shoda.
«≈» přibližnost. Strukturní rozdíl. Příklad: Dvě láhve o objemu 0,5 litru a 0,6 litru jsou si z dálky podobné, ale jejich rovnost je pouze vizuální, ve skutečnosti je však zkreslená, strukturálně si podobné nejsou. Proto jsou čáry ve znaku přibližnosti zkreslené.
«↔️» harmonizováno. Dvě láhve mléka – stejný objem, hmotnost, mléko od jedné krávy, ale doba dojení je jiná, ráno a večer, takže molekulární složení je jiné, tj. láhve si nejsou rovny vnitřním složením.
Jiný příklad: +5 a -5 jsou harmonizovány vzhledem k souřadnicovému středu, tj. nejsou si rovny, ale vzhledem k nějaké struktuře jsou harmonizovány.
Dál si blíže rozebereme velmi zajímavé objemově-časové sčítání a násobení.
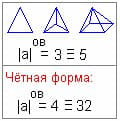
Pravidlo objemově-časového násobení: při objemově-časovém násobení bude mít obrazec tolik referenčních bodů, kolik původních struktur opakuje referenční body trojrozměrného obrazce.
Příklad: |a| = 3. To znamená, že dvourozměrný obrazec bude mít 3 body (trojúhelník). Trojrozměrný bude mít 4 referenční body. Objemově-časový obrazec tedy budou 4 navzájem spojené trojúhelníky (pyramida).
Je-li útvar sudý, |a| = 2 nebo 4. Dvourozměrný obrazec bude čtverec, trojrozměrný obrazec krychle (tj. 8 bodů), resp. objemově-časový obrazec bude mít 8 čtverců (tj. 32 bodů). Představte si kouli, na kterou je nalepeno 8 čtvercových zrcadel. Není to trojrozměrný, není to čtyřrozměrný obrazec, bude jakoby zkreslený v našem chápání, v našem prostoru.
Násobení „Na“, „Ždy“, „Ju“
3 na 7 = 21. Násobení „na“ – dvourozměrné (ploché).
3 х 7 = 28. Násobení „ždy“ – trojrozměrné (prostorové).
3 * 7 = 35. Násobení „ju“ – objemově-časové.
Ve všech třech příkladech je základ stejný (tři), ale určující symbol říká, o jaký druh násobení se jedná.
V prvním příkladu se jedná o trojúhelník, tj. 3 referenční body (3 na 7 = 21).
Ve druhém příkladu jde o čtyřstěn, tj. 4 referenční body (3 ždy 7 = 28).
Ve třetím příkladu je to jehlan, tj. 5 referenčních bodů (3 ju 7 = 35).
Např. v údolí je 7 pyramid, které jsou spojeny pouze zemí, na níž jsou postaveny, tj. jeden objem se v prostoru opakuje 7krát.
Příklad se sudým číslem:
2 na 2 = 4.
2 ždy 2 = 16 (tj. čtverec proměněný v krychli (8 bodů) a 2 krychle v prostoru jsou 16).
2 ju 2 = 64 (v první části máme, co je to za obrazec 8 čtverců (32 bodů), a tady jsou 2).
Objemově-časové násobení (Ju) bylo použito ve třech případech – při objemovém násobení, časovém násobení a objemově-časovém násobení. Toto násobení však nepočítá s objemy místnosti a dalších věcí, ale počítá s jinými objemy.
Objemově-časové sčítání. Při objemově-časovém sčítání se sčítá celé levé aktivum do jednoho čísla.
Příklad: 2 + 11 + 21 + 3 + 8 bude odpovídat 9.
V současné matematice by se všechna čísla sečetla do jednoho (45). V objemově-časovém sčítání se však sčítají jinak.
Za prvé: 2 + 11 = 13, tj. 4.
Dále: 4 + 21 = 25, což odpovídá 7.
7 + 3 = 10, což odpovídá 1.
1 + 8 = 9.
A na závěr, určení měrnosti pomocí přesně definovaných strukturálních obrazů.
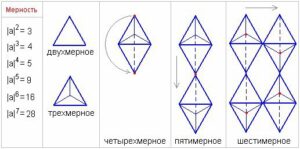
Nyní se budeme zabývat projekcí, pouze při mapování do ostré struktury, kde |a| dvourozměrné = 3, tj. tři referenční body. Abychom vám usnadnili vnímání, znázorníme si na dvojrozměrnosti ostrou strukturu – trojúhelník (viz. obr.).
Trojrozměrnost. Abychom získali trojrozměrnou strukturu, musíme promítnout tu dvojrozměrnou na všechny strany. Získáme tak 4 opěrné body.
Čtyřrozměrnost. Čtvrtý se počítá jakoby v čase, takže abychom získali čtyřrozměrný útvar, musíme promítnout strukturně (dva „tetrapaky“ spojené dnem). Získáme 5 opěrných bodů.
Pětirozměrnost. Čtyřrozměrný promítáme v prostoru, a to prostřednictvím jednoho společného bodu. Získáme 9 referenčních bodů.
Šestiměrnost. Šestiměrnostní strukturu získáme tak, že předchozí strukturu promítneme přes společné body. Získáme 16 referenčních bodů.
Sedmirozměrnost. Abychom získali sedmirozměrnou strukturu, je třeba na šestiměrnostní strukturu přes společné body (zvýrazněné červeně) nanést přesně stejnou strukturu. Získáme 28 referenčních bodů.
Zdroj:
t.me/sutinfa


